これから研究を始める高校生と指導教員のために 第2版
探究活動と課題研究の進め方・論文の書き方・口頭とポスター発表の仕方
(これ研)
副読文書
******* VIII-3. 一般化線形モデル入門 *******
説明変数が範疇の場合の、各条件間での平均値の差の解析
確率分布がポアソン分布の場合
--- 製造社間での、レーズンロールに入っている干し葡萄の平均数の差の解析 ---

「これから研究を始める高校生と指導教員のために 第2版;探究活動と課題研究の進め方・論文の書き方・口頭とポスター発表の仕方」(これ研)の第3部6.6節「一般化線形モデルの奨め」(p. 133)で紹介している一般化線形モデルを解説します。本章でも、説明変数が範疇の場合の、各条件間での平均値の差の解析の仕方を説明します。VIII-2章での解析と異なり、確率分布がポアソン分布の場合です。レーズンロールに入っている干し葡萄の数の解析を例に用います(「これ研」には載っていません)。A社・B社・C社・D社間で干し葡萄の数の平均に差があるのかどうかを検定します。「これ研」の第3部第6章「検定に挑戦しよう」(p. 118)を読み、検定とは何かを理解しておいて下さい。
RStudioを起動して下さい。起動方法の詳しい説明は、RStusioの起動の仕方を参照して下さい。そして、作業ディレクトリの指定の説明に従って作業ディレクトリを指定します。
setwd("/Users/sakai/Documents/書籍等原稿/これ研2版/課題研究解析")
# パソコン内での作業ディレクトリの位置がわかっている場合はこの方法が便利です。作業ディレクトリの位置の知り方は作業ディレクトリの表示を参照して下さい。あなたの作業ディレクトリの位置を""で囲んで書きます。この命令文を実行しておきます。
# 作業ディレクトリの位置がわからない(あるいは、上記の説明の意味がわからない)場合は、作業ディレクトリの指定の説明に従って指定して下さい。
解析と作図には、emmeansというものとtidyverseというものを用います。emmeans, tidyverseをインストールしてありますか? まだならば、下記の説明に従ってインストールして下さい。
install.packages("emmeans")
install.packages("tidyverse")
# RStudioを起動しこの命令文を実行します。emmeans, tidyverseを""で囲みます。作図の準備も参照して下さい。
インストールしたら、emmeans, tidyverseをRに読み込みます。
library(emmeans)
library(tidyverse)
# RStudioでこの命令文を実行しておきます。emmeans, tidyverseを""で囲みません。Rstudio起動後、一度だけ実行すればよいです。Rstudioを終了して再び起動したときは再実行する必要があります。
解析では、データフレームの中の特定のデータ列を指定することを行います。指定の方法です。
データフレーム名$データ列名
# データフレーム名を書き、$を挟んで、指定したいデータ列名を書きます。
# 実行例
d$Angle.degree
d$Flying.distance.m
# データフレームdに入っているデータ列Angle.degree, flying.distance.mを指定します。
1. 解析に用いるcsvファイルのRへの読み込み
レーズンロール内の干し葡萄数のデータがcsvファイル「Raisin.csv」(画面1)に入っています(架空データです)。製造社名(Maker)A, B, C, Dと、レーズンロールに入っている干し葡萄の数(Number)のデータです。各社につき100個のレーズンロールのデータがあります。このファイルをダウンロードして下さい。
画面1
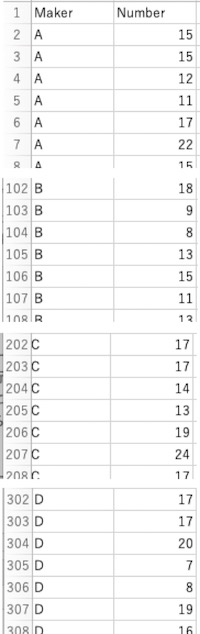
そして、ダウンロードしたファイルをあなたの作業ディレクトリに入れて下さい(「作業ディレクトリの指定」を参照)。
ご自身のデータを用いる場合は、そのデータが入ったcsvファイルを作業ディレクトリに入れて下さい。先頭行は必ずデータ名にして、続く行に個々のデータを書いて下さい。すべて、半角英数字で書いて下さい(日本語を入れない)。Excelで作ったファイルをcsvファイルに変換する方法は、Excelで作った解析用ファイルのcsv形式での保存を参照して下さい。
csvファイルをRに読み込み、データフレームに格納します。
d <- read.csv("Raisin.csv")
# csvファイル「Raisin.csv」を読み込んでデータフレームdに格納します。ファイル名を""で囲みます。ファイル名の拡張子「.csv」も忘れずに書きます。
# データフレームの名称(この例ではd)はお好みのものでよいです。
製造社名A, B, C, Dの並び順はこのままでよいでしょう。だから並び順の指定はしません。指定したい場合は、データの並び順の指定を参照して下さい。
2. 一般化線形モデルによる解析
一般化線形モデル実行の手順に従って一般化線形モデルを実行します。
2.1. 確率分布はポアソン分布に
適用する確率分布を指定します。確率分布とはと確率分布の説明を読んで下さい。レーズンロールに入っている干し葡萄の数はポアソン分布をすると考えられます。ロール内のある部位に干し葡萄が存在する確率は低いですが、存在しうる部位は、ロール内の全てという広い空間です。ポアソン分布の条件に合っています。
下の説明に従い、干し葡萄数のヒストグラムを描いてみましょう。
画面2
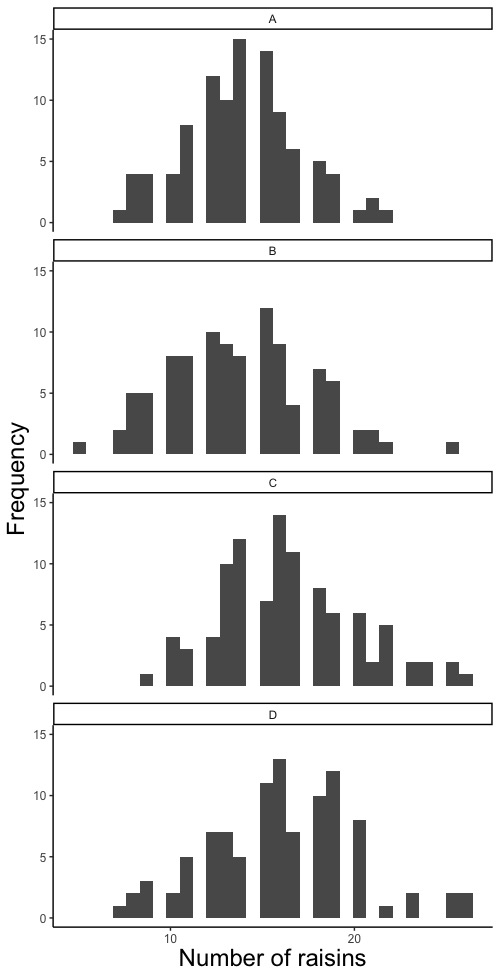
平均値がそれなりに大きい場合は、ポアソン分布は正規分布に似ています。
# 命令文が続く場合には+で繋げ、最後の命令文の後には+を付けません。
# 必須命令文
ggplot(d, aes(x = Number)) +# データフレームdを指定します。
# x = Numberとして、ヒストグラムを描く干し葡萄数のデータ列Numberをx軸(横軸)に指定します。xは小文字です。
# 末尾の+を忘れないで下さい。
# ヒストグラムにおける、作図に用いるデータフレームとデータの指定
geom_histogram() +
# 描く図としてヒストグラムを指定します。
# 末尾の+を忘れないで下さい。
facet_wrap(~ Maker, ncol = 1) +
# 複数の図を並べて描く場合はfacet_wrap()と命令します。
# データ列Makerに入っている製造社ごとにヒストグラムを描きます。Makerの前の~を忘れずに書いて下さい。
# 図の並べ方をncol(またはnrow)で指定します。ncol=1にすると縦1列に並びます。
# 末尾の+を忘れないで下さい。ただし、以降の命令文を省略する場合は+を付けず、「facet_wrap(~ Maker, ncol = 1)」とします。
# 省略してもよい命令文
# 以降の命令文を省略するとデフォルトで自動で描きます。
labs(x = "Number of raisins", y = "Frequency") +
# x軸(横軸)の名称をNumber of raisinsに、y軸(縦軸)の名称をFrequencyにします。名称を""で囲みます。x, yは小文字です。
scale_y_continuous(limits = c(0, 15)) +
# y軸(縦軸)を描く範囲を0から15に指定します。ヒストグラムの場合は、y軸の最小値を必ず0にします。
theme_classic() +
# 図の背景色を白にします。
theme(
axis.title.x = element_text(size = 18),
axis.text.x = element_text(size = 9),
axis.title.y = element_text(size = 18),
axis.text.y = element_text(size = 9)
)
# x軸(横軸)・y軸(縦軸)の名称(axis.title.x, axis.title.y)の文字の大きさを18に、x軸・y軸の目盛り(axis.text.x, axis.text.y)の文字の大きさを9に指定します。
ヒストグラムの描き方の詳しい説明はメダカの体長のヒストグラムを参照して下さい。図の軸の説明の文字を日本語にしたい場合は、その方法も、メダカの体長のヒストグラムを参照して下さい。
2.2. 連結関数は比例(identity)に
適用する連結関数を指定します。説明変数の値と応答変数の平均値の関係性:連結関数を用いた解析と適用する連結関数の指定の説明を読んで下さい。説明変数が範疇の場合は必ず比例(identity)を指定します。説明変数に0, 1という数値を与え、それらを直線で結ぶ回帰式を計算するからです。この回帰式は比例の式です。
2.3. 一般化線形モデルの実行
一般化線形モデルの命令文を実行します。一般化線形モデルの命令文の実行の説明を読んで下さい。説明変数が範疇で、比較する対象がA, B, C, D社の4つあります。なので、1. 一般化線形モデルの命令文および2. 追加命令文を実行します。
r <- glm(formula = Number ~ Maker, family = poisson(link = identity), data = d)
summary(r)
# 一般化線形モデルの命令文を実行して、その結果をデータフレームrに格納します。
# 解析するデータフレーム;d
# 応答変数;干し葡萄の数(Number)
# 説明変数;製造社(Maker)
# 確率分布;ポアソン分布(poisson)
# 連結関数;比例(identity)
# summary(r)を実行して、解析結果rの詳細を表示させます。
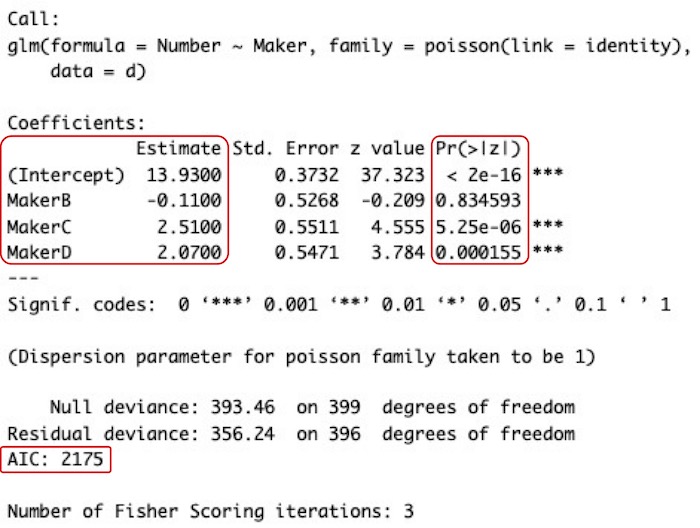
# 左上の赤枠内にあるのが、各社における平均干し葡萄数を示す数値です(ただしB社以降では、平均干し葡萄数そのもではありません)。各社の平均干し葡萄数は以下のようになります。
A社の平均干し葡萄数 = (Intercept) = 13.9300
B社の平均干し葡萄数 = MakerB + (Intercept) = - 0.1100 + 13.9300 = 13.82
C社の平均干し葡萄数 = MakerC + (Intercept) = 2.5100 + 13.9300 = 16.44
D社の平均干し葡萄数 = MakerD + (Intercept) = 2.0700 + 13.9300 = 16.00
連結関数が比例なので、y = ax + b (y;応答変数の平均値 x;説明変数の値 a;傾きの値 b;切片の値)という形で応答変数の平均値を示します。このとき、データの並び順の先頭に出てくるもの(この例ではA社)の平均値を切片(Intercept)として扱います。つまり切片b(Intercept)の値がA社の平均干し葡萄数です。他社(B~D社)の平均値は、x = 1のときの値、すなわちy = a + bとして表現します。このとき、A~D社の平均干し葡萄数すべてを1つの回帰式に組み込むのではなく、「A社とB社の平均干し葡萄数の回帰式」「A社とC社の平均干し葡萄数の回帰式」「A社とD社の平均干し葡萄数の回帰式」という別々の回帰式を計算します。そして、各回帰式にx = 1を当てはめた値y = a + bを求めます。左上の赤枠内の2行目以降が、その社の回帰式のa(傾き)の値です。これに、A社の平均干し葡萄数(切片bの値)を加えた値がその社における平均干し葡萄数です。
# 右上の赤枠内にあるのがP値です。並び順の先頭(A社)に関しては、切片(Intercept)の値(bの値)が有意に0と異なるのかどうかを示しています。他のもの(B, C, D社)に関しては、切片の値との差(aの値)が有意に0と異なるのかどうかを示しています。「e-」とあるのは10のマイナス何乗かということです。「2e-16」は「2 × 10- 16」で、「5.25e-06」は「5.25 × 10- 6」です。
A社の平均干し葡萄数(Intercept)のP値;2 × 10- 16 有意に0と異なる。
A社とB社の平均干し葡萄数の差のP値;0.834593 有意に0と異ならない。つまり、A社とB社の平均干し葡萄数に差があるとは言えない。
A社とC社の平均干し葡萄数の差のP値;5.25 × 10- 6 有意に0と異なる。つまり、A社とC社の平均干し葡萄数に有意な差がある。平均干し葡萄数は、A社が13.9300でC社が16.44であり、C社の方が有意に多い。
A社とD社の平均干し葡萄数の差のP値;0.000155 有意に0と異なる。つまり、A社とD社の平均干し葡萄数に有意な差がある。平均干し葡萄数は、A社が13.9300でD社が16.00であり、D社の方が有意に多い。
# 下の赤枠内の数値がAICです。AICによる、確率分布と連結関数の選択を参照して下さい。確率分布を、正規分布やガンマ分布にするとAICが2175よりも大きくなります。ポアソン分布が確かに合っているということです。
# 上記の解析では、B, C, D社間での平均干し葡萄数の差を検定できていません。そのため、2. 追加命令文を実行してこれらの間での差を検定します。
# 比較の対象が2つだけの場合は2. 追加命令文は不要で、これで解析は終わりです。たとえば、A社とB社のデータしかなく、この2つの間での差のみを検定したい場合などです。上記の解析で両者の差(B社と、切片(Intercept)であるA社の差)が検定できているので、これ以上の解析は必要ありません。
pairs(emmeans(r,"Maker"), adjust="holm")
# 1. 一般化線形モデルの命令文の実行結果がデータフレームrに格納されています。
# データフレームrと説明変数Makerを指定します。Makerを""で囲みます。
# A, B, C, D社間で、平均値の有意差を総当たりで検定します。切片となる製造社(データの並び順で先頭になるもの)を自動的に入れ替え、その切片との比較をしてくれます。
# adjust="holm"を忘れずに書いて下さい。
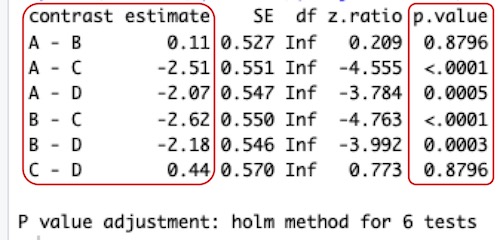
# 実行結果です。左の赤枠内にあるのが、製造社の各組合せでの平均干し葡萄数の差です。contrastが製造会社の組合せ、estimateが干し葡萄数の差です。
# 右の赤枠内にあるのが平均値の差のP値です。平均値に有意に差があるのかどうかを示しています。
# A社とB社の差のP値が0.8796になっています。ところが1. 一般化線形モデルの命令文の実行の方では、このP値は0.834593です。A社とC, D社との差もP値が変わっています。変ですね。その理由を、多重比較における補正で説明しています。この説明を必ず読んで下さい。
# P値はすべて、この追加命令文によって得た値を採用して下さい。A社との比較のP値は1. 一般化線形モデルの命令文でも出ていますが、それらではなく、2. 追加命令文で得た値を採用します。
# 追加命令文
3. 作図
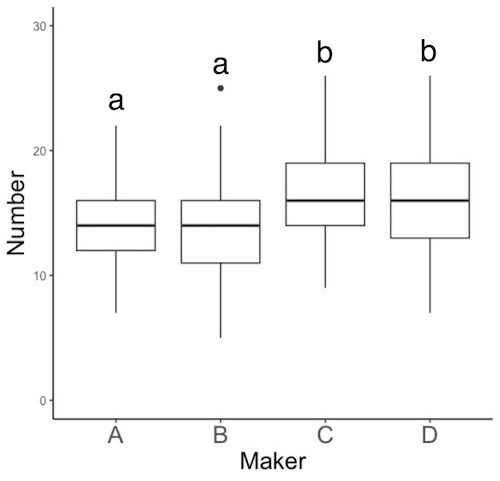
検定結果を作図する方法を説明します。ヒストグラム(画面2)でもよいのですが、スペースを節約するために箱ひげ図にしましょう。
画面3
# 命令文が続く場合には+で繋げ、最後の命令文の後には+を付けません。
# 必須命令文
ggplot(d, aes(x = Maker, y = Number)) +
# データフレームdを指定します。
# x = Makerとして、製造社名(Maker)が入っているデータ列Makerをx軸(横軸)に指定します。xは小文字です。
# y = Numberとして、干し葡萄の数(Number)が入っているデータ列Numberをy軸(縦軸)に指定します。yは小文字です。
# データ列Makerに入っている製造社ごとに、データ列Numberに入っている干し葡萄の数のデータを作図します。
# 末尾の+を忘れないで下さい。
# 箱ひげ図における、作図に用いるデータフレームとデータの指定
geom_boxplot() +
# 描く図として箱ひげ図を指定します。
# 末尾の+を忘れないで下さい。ただし、以降の命令文を省略する場合は+を付けず、「geom_boxplot()」とします。
# 箱ひげ図の指定
# 省略してもよい命令文
# 以降の命令文を省略するとデフォルトで自動で描きます。
labs(x = "Maker", y = "Number") +
# x軸(横軸)の名称をMakerに、y軸(縦軸)の名称をNumberにします。名称を""で囲みます。x, yは小文字です。
scale_y_continuous(limits = c(0, 30)) +
# y軸(縦軸)を描く範囲を0から30に指定します。
theme_classic() +
# 図の背景色を白にします。
theme(
axis.title.x = element_text(size = 18),
axis.text.x = element_text(size = 18),
axis.title.y = element_text(size = 18),
axis.text.y = element_text(size = 9)
)
# x軸(横軸)の目盛り(axis.text.x)には製造社名(A, B, C, D)が入っています。製造社名とx軸・y軸(縦軸)の名称(axis.title.y)の文字の大きさを18に、y軸の目盛り(axis.text.y)の文字の大きさを9に指定します。
箱ひげ図の詳しい描き方は、メダカの体長の箱ひげ図を参照して下さい。図の軸の説明の文字を日本語にしたい場合は、その方法も、メダカの体長の箱ひげ図を参照して下さい。
P値が0.05以下の製造社間では平均干し葡萄数に有意な差があると判定します。ここでいうP値は、比較の対象が3つ以上で複数組の検定を行った場合は補正後のもの(2. 追加命令文の実行で得たP値)、2つしかなく検定を1回しか行っていない場合は補正前のもの(1. 一般化線形モデルの命令文の実行で得たP値)です。そして以下のようにアルファベットを添えます(PowerPoint等に読み込んで書き込みます)。
平均に有意な差がないもの;同じ文字を添える
平均に有意な差があるもの;異なる文字を添える
画面4
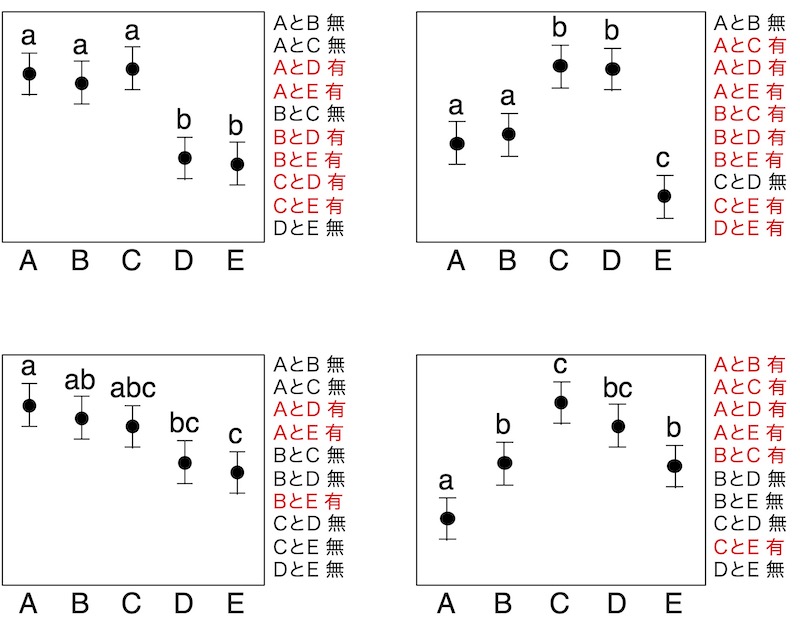
検定結果が複雑だと、1つの平均値に複数の文字を添えて差の有無の範囲を示すことになります。この場合、結果の理解もちょっと面倒です。たとえば右下の場合、「CとDに有意差なし」「DとEに有意差なし」です。ならばCとEにも差がないと思ってしまいそうですが、「CとEには有意差あり」です。検定の結果を正確に理解して下さいね。