これから研究を始める高校生と指導教員のために 第2版
探究活動と課題研究の進め方･論文の書き方･口頭とポスター発表の仕方
(これ研)
副読文書
VIII-1. 一般化線形モデル入門
一般化線形モデルで行うこと
(｢これ研｣本文の第3部6.6節；p. 133)
｢これから研究を始める高校生と指導教員のために 第2版；探究活動と課題研究の進め方･論文の書き方･口頭とポスター発表の仕方｣(これ研)の第3部6.6節｢一般化線形モデルの奨め｣(p. 133)で紹介している一般化線形モデルを解説します。｢これ研｣の第3部第6章｢検定に挑戦しよう｣(p. 118)を読み、検定とは何かを理解しておいて下さい。
本章では、一般化線形モデルとはどういうものなのかを説明します。
解析では、emmeansというものを使うことがあります。あらかじめ、emmeansをインストールして読み込んでおきましょう。
# RStudioを起動して、emmeansをインストールします。emmeansを""で囲みます。
library(emmeans)# emmeansを読み込みます。Rstudio起動後、一度だけ実行すればよいです。Rstudioを終了して再び起動したときは再実行する必要があります。
1. 一般化線形モデルの解析の目的
一般化線形モデルを用いた解析の目的は、条件に依存して、あるデータの値の平均値がどのように変化するのかを調べることです。たとえば、以下のようなことを調べます。下に出てくる説明変数とは原因となる条件のことで、応答変数とは、それに依存して値が変化するもののことです。
◇ 発射角度という条件(説明変数)に依存して、ペットボトルロケットの飛行距離(応答変数)の平均値がどのように変化するのか。
◇ 生育地という条件(説明変数)に依存して、メダカの体長(応答変数)の平均値がどのように変化するのか。
◇ 体長という条件(説明変数)に依存して、メダカの産卵数(応答変数)の平均値がどのように変化するのか。
◇ 単語の記憶時間帯(就寝前か起床後か)という条件(説明変数)に依存して、単語の記憶試験(応答変数)の平均値がどのように変化するのか。
◇ 生育場所の明るさという条件(説明変数)に依存して、植物の茎の高さ(応答変数)の平均値がどのように変化するのか。
こうした研究で取るデータにはどうしたって偶然性が伴います。たとえばメダカの体長が、東北では33.2±5.3mm(平均±標準偏差)で九州では31.5±4.9mmという結果を得たとします。しかしもう一度調査をやり直したら、東北では32.5±5.0mmで九州では32.8±5.1 mmなどと結果が逆転するかもしれません。そのため、生育地に依存して体長が変化するのかどうか、はっきりしたことが言えないかもしれません。
こうした偶然性を排除し、条件に依存して平均値が本当に変化するのかどうかを調べる必要があります。つまり、母集団において依存性が見られるのかどうかを推定する必要があります。一般化線形モデルは、そのための強力な統計手法です。
2. 確率分布とは
統計解析(一般化線形モデルに限らず)を行う上で重要な確率分布というものを説明します。ある同じ条件の研究対象(母集団)から複数個のデータを取っても、ほとんどすべての場合、取ったデータの値にばらつきがあります。データの値がそもそもばらつく対象(｢これ研｣本文の第3部第3章参照；p. 83)ではもちろんのこと、唯一の真の値があるはずの対象(｢これ研｣本文の第3部第2章参照 ;p. 71)でもばらつきます。どのようにばらつくのかは、母集団において、どういう値のものがどれくらい存在するのかによって決まります。
画面1
メダカの体長を例に考えてみます。画面1は、メダカの母集団を模式的に示したものです。メダカの体長は連続的に変化し、色々な体長の個体が母集団に存在します。ある体長の個体がどれくらいの割合で存在するのかを示してみましょう(画面1右上)。実際には体長は連続的に変化するのですが、7つの体長を示しています。この母集団から無作為にデータを取るとすると、ある体長のデータを取る確率は、母集団内でのその体長の個体の存在割合に等しいです。その確率を、存在しうる全体長に対してまとめたものが確率分布です(画面1の下)。データを取るとは、母集団から無作為に値を引くということです。確率分布は、その値を引く確率、つまり、データがその値になる確率をまとめたものです。
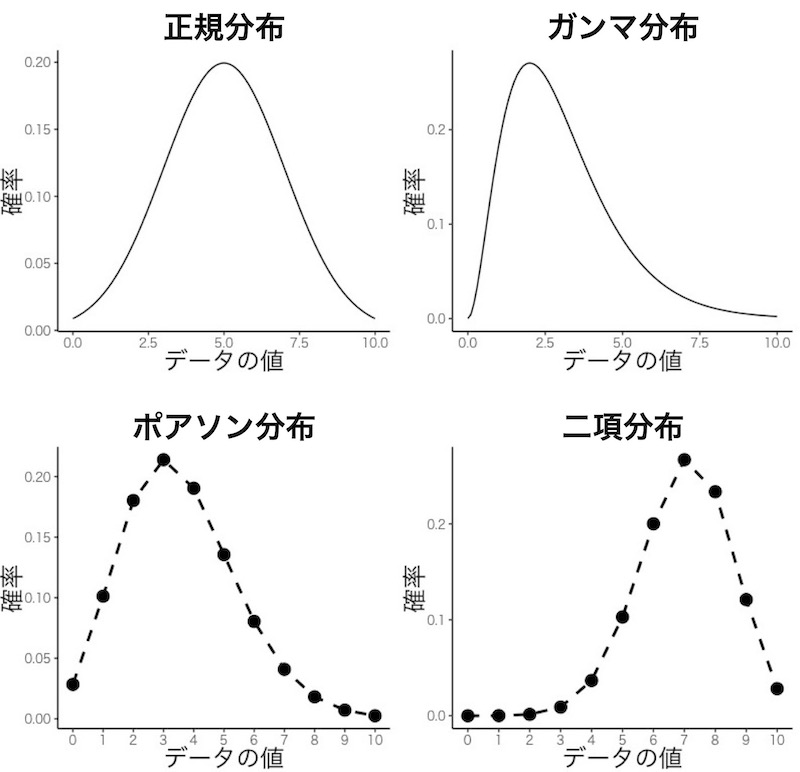
確率分布には色々な型があります。つまり、その値になる確率のグラフの形に色々なものがあるということです。
画面2
どの型の確率分布をとるのかは、データを取る対象に応じて決まります。
1) それが起きる確率は低い。
2) しかし、起きうる機会はたくさんある。
サッカーなど、時間内に点を取り合うスポーツの得点･液体中の微生物の数･工業製品の不良品の数などがポアソン分布をします。たとえばサッカーの得点は、なかなか入らない(起きる確率が低い)けれど、90分という長い時間があります。液体中の微生物の数も、ある特定の場所に個体がいる確率は低いけれど、存在しうる空間は十分にあります。このように、上記の2つの条件を満たすものは多いです。
・硬貨を10回投げたときにx回(x = 0, 1, 2, 3, ..., 10)表になる確率
・20個の種子のうちx個(x = 0, 1, 2, 3, ..., 20)が発芽する確率
・ミドリムシ20個体の内、明るい方向にx個体(x = 0, 1, 2, 3, ..., 20)が移動する確率
データの値(上記のxの値)として取りうるのは、0, 1, 2, 3,...という0以上の整数値です。
検定では、取ったデータの平均値がその値になる確率を計算します(詳しくは、｢これ研｣の本文第3部第6章参照；p. 118)。この確率の計算値は、確率分布の型が異なると変わります。その研究対象にあてはまる確率分布の元で計算しないと、検定結果も間違ったものになってしまいます。
そのため統計解析ではまず、その研究対象が、どういう型の確率分布をとっているのかを推定します。次に、その確率分布を適用できる統計手法を選択します。たくさんの検定手法があるのですが、特定の確率分布にしか適用できないものが多いのです。たとえばt検定は、正規分布にしか適用できません。
一般化線形モデルの特徴は、画面2にあるようなさまざまな確率分布に適用できることです。高校生が扱うデータのほとんどに適用できるはずです。あなたの研究対象がとっている確率分布を指定して、一般化線形モデルの解析を行います。汎用性のある強力な統計手法です。
3. 条件に依存した平均値の変化
では、どのようにして、条件に依存した平均値の変化を解析するのでしょうか。説明変数が範疇の場合(単語記憶時間が就寝前か起床後かや、生育場所が明るいか暗いかの二択の場合など)と数値の場合(植物の茎の高さやメダカの体長など)それぞれについて説明します。
3.1. 説明変数が範疇の場合
明るい場所と暗い場所(説明変数)において、植物の茎の高さ(応答変数)の平均値に差があるのかどうかを調べる研究を例に説明します。
画面3
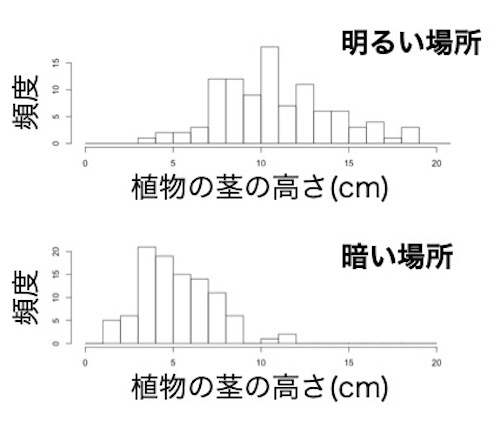
調査したところ、画面3のヒストグラムが得られました(架空データです)(ヒストグラムの描き方)。
まずは、確率分布の型を推定します。ヒストグラムでデータ分布の形を見みます。確率分布とはの説明も参照します。このデータの確率分布はガンマ分布です(正規分布にも見えますが；あくまでも説明の例なので、どちらなのか気にしないで下さい)。
画面4
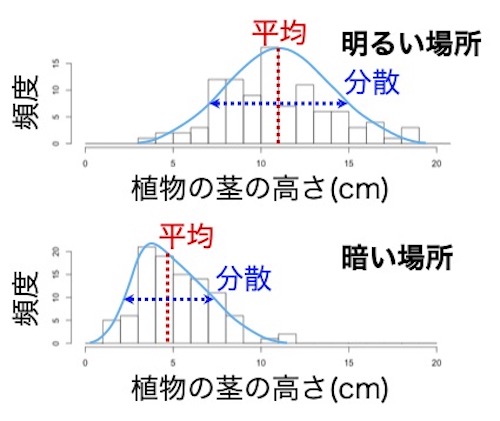
その確率分布をヒストグラムに描き込んでみました。平均と分散をデータから計算しています。分散は、データの値がどれだけばらついているのかを示す指標です。値が大きいほどばらつきが大きいです。
知りたいのは、明るい場所と暗い場所で、茎の高さの平均値に本当に差があるのかどうかです。こうした研究では、説明変数を横軸にし応答変数を縦軸にして、説明変数(明るさ)への応答変数(茎の高さ) の依存性を見ます。この図もそのように描き直してみましょう。
画面5
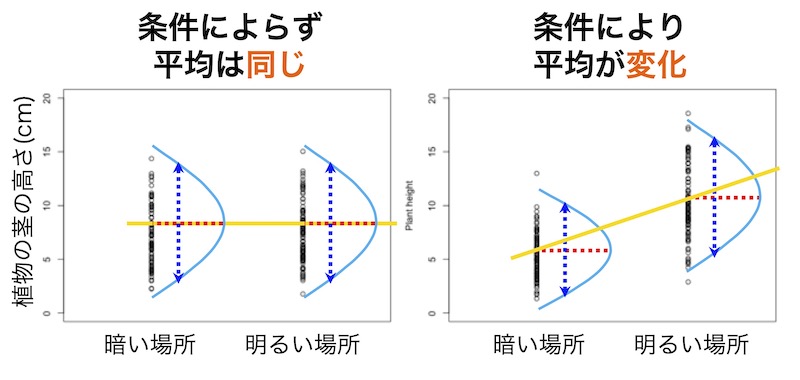
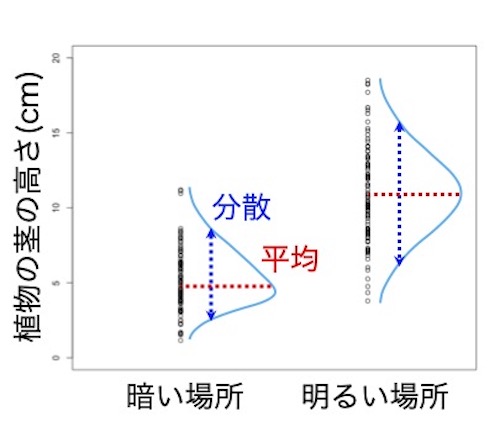
説明変数である明るさを横軸に並べ、目的変数である茎の高さを縦軸にしました。1つ1つの○がデータ値です。
依存性を見るために回帰式を求めます。明るさ(説明変数)に依存して、茎の高さ(応答変数)の平均値がどう変化するのかを示した式です。仮の数値として、暗い場所に0を、明るい場所に1を与え、明るさを数値化して回帰式を求めます。
画面6
画面6の黄色い直線が回帰式です。その傾きが0(左図)ならば、茎の高さの平均値は明るさに依存しません。正ならば明るいほど高く(右図)、負ならば明るいほど低いと判定できます。
このように、説明変数に対する応答変数の平均値の回帰式を求め、その傾きが0なのか正なのか負なのかを調べるのが一般化線形モデルの基本です。正確には、傾きが0から有意に異なるのかどうかを検定します(検定の考え方については｢これ研｣の本文第3部第6章参照；p. 118)。つまり、傾きが0である母集団から標本を取ったときに偶然にその傾きになる確率を計算し、その傾きになることがどれだけ稀なのかを調べます。傾きが0から有意に異なるのなら正(負)の依存性があると判定し、有意に異ならないのなら依存性があるとは言えないと判定します。
こうした検定において重要なのが、母集団においては依存性がない(回帰式の傾きが0)の時に、取ったデータにおいては偶然に依存性が生じる(回帰式の傾きが正または負となる)確率の計算です。この確率は、確率分布の型によって変わります。ですから、その研究対象がとっている確率分布を正しく選定する必要があります。
3.2. 説明変数が数値の場合
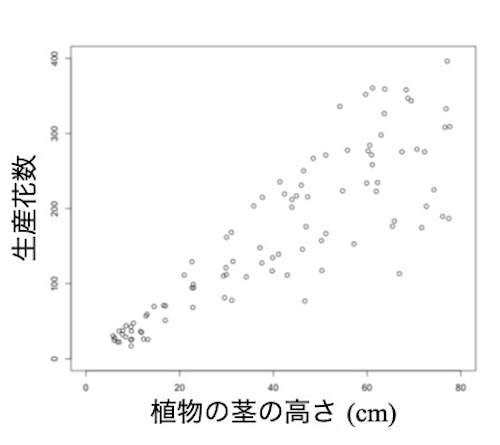
説明変数が数値の場合も行うことはほとんど同じです。植物の茎の高さ(説明変数)に依存して、その個体の生産花数(応答変数)の平均値がどのように変化するのかを調べるとします。
画面7
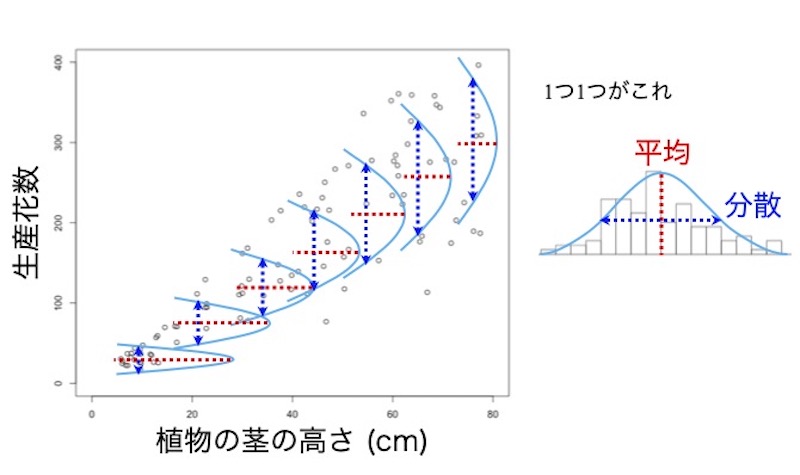
説明変数が範疇の場合との違いは、説明変数の値が連続的に変化していることだけです。つまり画面8のようになっているのです。
画面8
説明変数(この例では植物の茎の高さ)のある一つの値に対して、画面8の右側に添えた図のような、応答変数(この例では生産花数)のデータの分布が存在します。これが連続的に存在しているわけです。
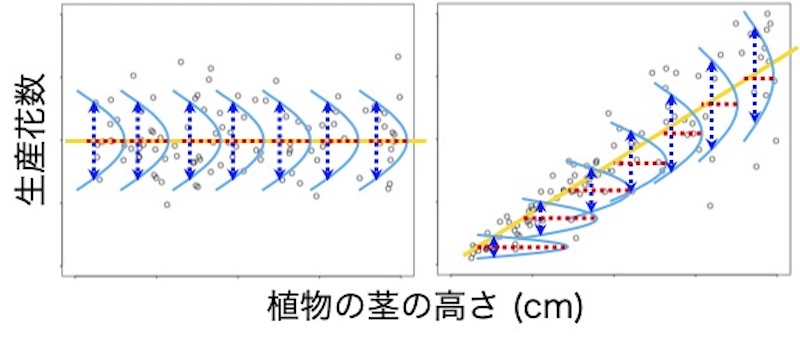
依存性を見るために回帰式を求めます。茎の高さ(説明変数)に依存して、生産花数(応答変数)の平均値がどう変化するのかを示した式です。説明変数が数値なので、(範疇の場合のように0, 1という仮の値を与えることなく)説明変数の値をそのまま使って計算します。
画面9
画面9の黄色い直線が回帰式です。その傾きが0(左図)ならば、生産花数の平均値は茎の高さに依存しません。正ならば、茎が高いほど花数が多く(右図)、負ならば、茎が高いほど花数が少ないと判定できます。
このように数値の場合も、説明変数に対する応答変数の平均値の回帰式を求め、その傾きが0なのか正なのか負なのかを調べます。正確には、傾きが0から有意に異なるのかどうかを検定します(検定の考え方については｢これ研｣の本文第3部第6章参照；p. 118)。この検定でももちろん、その研究対象がとっている確率分布を正しく選定することが大切です。
4. 説明変数の値と応答変数の平均値の関係性：連結関数を用いた解析
一般化線形モデルのもう一つの特徴を説明します。説明変数の値と応答変数の平均値の関係性を考えてみましょう。説明変数が数値の場合で用いた例では、応答変数(生産花数)の平均値が説明変数(茎の高さ)の値に比例的に依存していました。つまり、y = ax + b (x；説明変数の値 y；応答変数の平均値)という一次式で回帰していました。しかし、説明変数の値と応答変数の平均値の関係は他にもありえます。
画面10
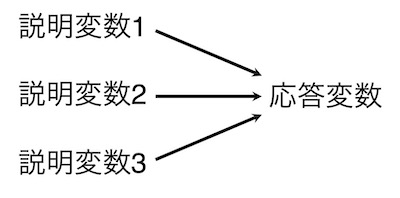
比例； y = ax + b
指数； y = eax + b
S字； y = eax + b/(1 + eax + b)
反比例； y = 1/(ax + b)
x；説明変数の値
y；応答変数の平均値
a, b; 定数
e；自然対数の底
正確な解析を行うためには、両者の関係性に応じて回帰式を使い分ける必要があります。一般化線形モデルならばこの使い分けが可能です。つまり一般化線形モデルには、画面10のような色々な関係性を解析できるという強みがあります。
回帰式の使い分けのために連結関数というものを用います。連結関数は、上記の回帰式の右辺を一次式(ax + bという形)に変形すると出てくるものです。こうした変形を行うのは、一般化線形モデルの解析の都合上必要だからです。
比例； y = ax + b (これはこのまま)
指数； loge y = ax + b
S字； loge y/(1 - y) = ax + b
反比例； 1/y = ax + b
変形して出てきた左辺(y, loge y, loge y/(1 - y), 1/y)を連結関数といいます。つまり連結関数は、説明変数の値と応答変数の平均値の関係性を示したものです。関係性に応じて連結関数を使い分けることで、色々な場合を解析できます。
説明変数が数値の場合、連結変数は、比例･指数･S字･反比例のいずれもとりえます。範疇の場合は比例のみです。上述のように、x = 0, 1を仮の数値として与えて、それらを直線で結ぶ回帰式を計算するからです。この回帰式は比例の式です。
5. 一般化線形モデル実行の手順
Rを使って一般化線形モデルを実行する手順です。
以下で、手順を説明します。
5.1. 解析したいデータのデータフレームへの格納
解析したいデータをExcelで作り、CSVコンマ区切り(.csv)で保存します。そのcsvファイルをRに読み込んでデータフレームに格納します。これらの方法は、ExcelのファイルのRへの読み込み方を参照して下さい。
5.2. 説明変数と応答変数の指定
説明変数(原因となる条件)と応答変数(説明変数に依存して値が変化するもの)を指定します(一般化線形モデルの解析の目的を参照)。
複数の説明変数を指定することができます。複数の要因が応答変数に影響している可能性があり、それら複数の要因の影響を解析することもあるでしょう。たとえば、ペットボトルロケットの飛行距離には、発射角度だけでなく、ボトル内に入れた水量も関係します。発射角度と水量を変えて実験を行った場合は、この二つが説明変数となります。
画面11
こうした場合は、説明変数を複数指定して解析します。説明変数は、範疇･数値のどちらでもよいですし、両者が混ざっていてもよいです。ただし、複数の説明変数を指定する解析は難しく、高校生が行うこともあまりないようです。そのため本文書ではその解析方法の説明はしません。複数指定ができるということだけ知っておいて下さい。
5.3. 適用する確率分布の指定
確率分布を指定します。確率分布とはを参照して、あなたの応答変数のデータ分布に合ったものを指定して下さい。応答変数のヒストグラムを描き、どういうデータ分布をしているのかを見ることも大切です。描く方法は、メダカの体長のヒストグラムを参照して下さい。
確率分布と連結関数には使える組合せがあります(下の黒枠内を参照)。その確率分布で指定できる連結関数を選んで下さい。
確率分布の指定のためにAICという数値も参照します。詳しくは、AICによる、確率分布と連結関数の選択を参照して下さい。
| 命令文中で用いる 関数名 |
取りうる値(y)の範囲 | 適用できるデータ | 指定できる連結関数 | |
|---|---|---|---|---|
| 正規分布 | gaussian | – ∞ < y < ∞ | 左右対称の釣り鐘型 | identity(比例) log(指数) inverse(反比例) |
| ガンマ分布 | Gamma | 0 < y < ∞ | 左右非対称で、 値が大きい方に尾を引く |
inverse(反比例) identity(比例) log(指数) |
| ポアソン分布 | poisson | 0以上の整数 上限なし |
上限のない整数値 | log(比例) identity(比例) |
| 二項分布 | binomial | 0以上の整数 上限あり |
n回のうち、あることが起きる回数 nが上限 |
logit(S字) log(指数) |
主な確率分布を示しています。他の確率分布もあります。
確率分布とはも参照して下さい。
5.4. 適用する連結関数の指定
連結関数を指定します。説明変数の値と応答変数の平均値の関係性：連結関数を用いた解析を参照して、あなたのデータにあったものを指定して下さい。説明変数と応答変数の散布図を描き、説明変数に応答変数がどのように依存しているのかを見ることも大切です。描く方法は、メダカにおける、体長と産卵数の関係を参照して下さい。
連結関数と確率分布には使える組合せがあります(下の黒枠内を参照)。その連結関数で指定できる確率分布を選んで下さい。
連結関数の指定のためにAICという数値も参照します。詳しくは、AICによる、確率分布と連結関数の選択を参照して下さい。
| 命令文中で用いる 関数名 |
連結関数の形 | 説明変数への依存性 | 指定できる確率分布 | |
|---|---|---|---|---|
| 比例 | identity | y | 比例して増える | gaussian(正規分布) Gamma(ガンマ分布) poisson(ポアソン分布) |
| 指数 | log | loge y | 指数で増える | gaussian(正規分布) Gamma(ガンマ分布) poisson(ポアソン分布) binomial(二項分布) |
| S字 | logit | loge y/(1 - y) | S字で増える | binomial(二項分布) |
| 反比例 | inverse | 1/y | 反比例で減る | gaussian(正規分布) Gamma(ガンマ分布) |
主な連結関数を示しています。他の連結関数もあります。
y；応答変数の平均値 e；自然対数の底
説明変数の値と応答変数の平均値の関係性：連結関数を用いた解析も参照して下さい。
5.5. 一般化線形モデルの命令文の実行
命令文を実行します。1. 一般化線形モデルの命令文と2. 追加命令文の2つがあります。説明変数がどういうものかに応じて以下のように使います。
1. 一般化線形モデルの命令文および2. 追加命令文を実行します。
1. 一般化線形モデルの命令文のみを実行します。
たとえば、東北･関東･関西･九州のメダカを比較する場合は、比較対象が4つなので追加命令文が必要です。東北と関東のメダカのみを比較する場合は、比較対象が2つなので追加命令文の実行は不要です。
説明変数が数値の場合も追加命令文の実行は不要です。たとえば、メダカの体長と産卵数の関係を調べる場合、説明変数である体長は連続的に変化する数値です。この場合、一般化線形モデルの命令文のみを実行すればよいです。
説明変数が｢数値｣の形をとっていても、範疇として扱うこともあります。たとえば、ペットボトルロケットの飛行距離を発射角度25, 30, 35, 40, 45間で比較する場合、｢25度｣｢30度｣｢35度｣｢40度｣｢45度｣という条件間での比較となります。こうした比較は、｢明るい場所｣と｢暗い場所｣の比較といった範疇間での比較と同質です。そのため、説明変数は範疇であるとします。比較の対象が3つ以上の場合は追加命令文の実行が必要となります(2つの場合は不要です)。
解析の実行例は、VIII-2章, VIII-3章, VIII-4章, VIII-5章, VIII-6章を参照して下さい。
glm(formula = 応答変数 ~ 説明変数, family = 確率分布(link = 連結関数), data = データフレーム名)
# 実行例
r <- glm(formula = Length.mm ~ Locality, family = gaussian(link = identity), data = d)
summary(r)
# メダカの体長を地域間で比較します。データフレームdに、体長(Length.mm)と生育地域(Locality)のデータが格納されています。
# 応答変数；体長(Length.mm)
# 説明変数；生育地域(Locality)
# 確率分布；正規分布(gaussian)
# 連結関数；比例(identity)
# 一般化線形モデルによる解析結果をデータフレームrに格納します。
# summary(r)を実行して、解析結果rの詳細を表示させます。
r <- glm(formula = Egg.number ~ Length.mm, family = Gamma(link = log), data = d)
summary(r)
# メダカの体長と産卵数の関係を調べます。データフレームdに、産卵数(Egg.number)と体長(Length.mm)のデータが格納されています。
# 応答変数；産卵数(Egg.number)
# 説明変数；体長(Length.mm)
# 確率分布；ガンマ分布(Gamma)
# 連結関数；指数(log)
# 一般化線形モデルによる解析結果をデータフレームrに格納します。
# summary(r)を実行して、解析結果rの詳細を表示させます。
説明変数が範疇で、比較する対象が3つ以上の場合のみ実行します。emmeansをインストールして読み込んでおく必要があります(emmeansのインストールと読み込みを参照)。
pairs(emmeans(解析結果を格納したデータフレーム名, "説明変数"), adjust = "holm")
# 前もって、一般化線形モデルの命令文を実行し、その解析結果をデータフレームに格納しておきます。
# 説明変数名を""で囲みます。
# adjust="holm"を忘れずに書いて下さい。holmを""で囲みます。
# 実行例
r <- glm(formula = Length.mm ~ Locality, family = gaussian(link = identity), data = d)
pairs(emmeans(r, "Locality"), adjust = "holm")
# メダカの体長を地域間で比較します。データフレームdに、体長(Length.mm)と生育地域(Locality)のデータが格納されています。
# 応答変数；体長(Length.mm)
# 説明変数；生育地域(Locality)
# 確率分布；正規分布(gaussian)
# 連結関数；比例(identity)
# 一般化線形モデルによる解析結果をデータフレームrに格納します。
# Localityに、Tohoku, Kanto, Kansai, Kyushuという4つの地域が入っています。各地域間で平均体長に差があるのかどうかを検定するために、pairs(emmeans(r,"Locality"), adjust="holm")を実行します。
5.6. AICによる、確率分布と連結関数の選択
どの確率分布と連結関数を適用すればよいのか迷うこともあると思います。その場合は、AICという数値を基準として選択します。AICについて詳しく説明はしませんが、要は、確率分布･連結関数がそのデータにどれだけ合っているのかの指標となるものです。一般化線形モデルを実行するとAICの値も出て来ます。正の値のみならず負の値になることもあります。値が小さいほど良いです。いろいろな組合せの確率分布･連結関数で実行してみて、AICが一番小さな組合せを採用して下さい。