これから研究を始める高校生と指導教員のために　第2版
探究活動と課題研究の進め方･論文の書き方･口頭とポスター発表の仕方
(これ研)

副読文書
VIII-5. 一般化線形モデル入門
1種類のデータにおけるデータ分布の偏りの解析
条件の変化の影響を見ない場合
ミドリムシの走光性の解析
　　(｢これ研｣の本文の第3部3.3.3項；p. 96)

私のサイトでの本書紹介文

　｢これから研究を始める高校生と指導教員のために　第2版；探究活動と課題研究の進め方･論文の書き方･口頭とポスター発表の仕方｣(これ研)の第3部6.6節｢一般化線形モデルの奨め｣(p. 133)で紹介している一般化線形モデルを解説します。本章では、1種類のデータを対象に、そのデータ分布に偏りがあるのかどうかの解析の仕方を説明します。ミドリムシの走光性実験で、明るい方と暗い方のどちらに移動するのかの検定を例に用います(｢これ研｣の本文第3部3.3.3項；p. 96)。｢これ研｣の第3部第6章｢検定に挑戦しよう｣(p. 118)を読み、検定とは何かを理解しておいて下さい。

　RStudioを起動して下さい。起動方法の詳しい説明は、RStusioの起動の仕方を参照して下さい。そして、作業ディレクトリの指定の説明に従って作業ディレクトリを指定します。

　作図にはtidyverseというものを用います。tidyverseをインストールしてありますか？ まだならば、作図の準備の説明に従ってインストールして下さい。インストールしたら、tidyverseをRに読み込みます。

　解析では、データフレームの中の特定のデータ列を指定することを行います。指定の方法です。

1. 解析に用いるcsvファイルのRへの読み込み

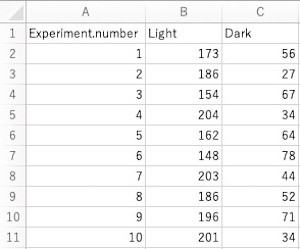
　csvファイル｢Light.csv」(画面1)に、ミドリムシの走光性実験の結果が入っています(架空データです)。Experiment.numberが実験番号(10回行った内の何回目か)、Lightが、明るい方に行った個体数、Darkが、暗い方に行った個体数です。このcsvファイルのデータを使って解析と作図を行います。

画面1

csvファイルをダウンロードして、あなたの作業ディレクトリに入れて下さい(｢作業ディレクトリの指定｣を参照)。

　ご自身のデータを用いる場合は、そのデータが入ったcsvファイルを作業ディレクトリに入れて下さい。Excelで作ったファイルをcsvファイルに変換する方法は、Excelで作った解析用ファイルのcsv形式での保存を参照して下さい。

　csvファイルをRに読み込み、データフレームに格納します。

2. 一般化線形モデルによる解析

　一般化線形モデル実行の手順に従って一般化線形モデルを実行します。

2.1. 確率分布は二項分布(binomial)に、連結関数はS字(logit)に

　本解析の場合、確率分布は二項分布(binomial)を、連結関数はS字(logit)を必ず指定します。

　確率分布が二項分布なのは明白です(確率分布とはを参照)。本解析における応答変数yは、明るい方(または暗い方)に移動する確率です。そして、明るい方に移動する確率をyとし、暗い方に移動する確率を1-yとしたときのyの値を解析します。これはまさに二項分布です。

　連結関数がS字なのは、応答変数であるyが確率であるため0以上1以下の値しか取らないからです(説明変数の値と応答変数の平均値の関係性：連結関数を用いた解析を参照)。連結関数がS字の場合、

y = e^{ax + b}/(1 + e^{ax + b})

という関係になっています(ただし、2.2. 本解析における説明変数で説明するように本解析の場合、axの部分はなくy = e^b/(1 + e^b)という式になります)。ax + bは、原理的には− ∞から∞の値を取りえます。ax + bが− ∞に近づくほどe^{ax + b}は0に近づき、そのためyも0に近づきます。しかし、0を下回ることはありません。かたや、ax + bが無限大に近づくほどyは1に近づきます。こちらも、1を超えることはありません。このようにS字は、応答変数が確率のときにぴったりな連結関数です。

2.2. 本解析における説明変数

　本解析における説明変数について説明します。

　本解析でデータとしてあるのは、ある1つの条件の下でのミドリムシの移動方向を調べた結果だけです。条件を変えると移動方向が変わるのかどうかを見ているわけではありません。

　これに対してこれまでの解析では、ペットボトルロケットの発射角度に依存した飛行距離の変化や、メダカにおける、体長の違いに依存した産卵数の違いなどを調べていました。発射角度･体長(説明変数)という条件の変化に対する応答変数の反応を解析したわけです。条件の変化は、説明変数ax + bのaxに現れます。xの値が変化すると応答変数がどのように応答するのかを解析するわけです。

　かたや、本解析のように1つの条件下でのデータしか無い場合は、説明変数が、その1つの条件のみの状態である解析となります。axという、条件に応じた変化の部分は存在しません。つまり説明変数は、ax + bではなくただのｂです。切片しかない説明変数ということです。連結関数はS字ですので、

y = e^b/(1 + e^b)

となります。切片bの値が、その1つの条件の影響を表します。

　解析では、切片bの値が0から有意に異なるのかどうかを検定します。b = 0の場合、

y = 1/2

です。明るい方と暗い方のどちらにも偏らず1/2の確率で移動するということです。bが0から有意に異なっていれば、どちらかに偏って移動すると判定できます。

2.3. 一般化線形モデルの実行

　一般化線形モデルの命令文を実行します。一般化線形モデルの命令文の実行の説明を読んで下さい。1. 一般化線形モデルの命令文のみを実行します。

1. 一般化線形モデルの命令文の実行

r <- glm(formula = cbind(Light, Dark) ~ 1, family = binomial(link = logit), data = d)
summary(r)

# 一般化線形モデルの命令文を実行して、その結果をデータフレームrに格納します。

# 解析するデータフレーム；d
# 応答変数；移動方向(cbind(Light, Dark))。データ列Lightに明るい方へ移動した個体数が、データ列Darkに暗い方へ移動した個体数が入っています。cbindを使ってデータを横方向に統合し、各実験回における、(明るい方に移動した個体数, 暗い方に移動した個体数)という組合せからなるデータを作ります。
# 説明変数；その実験条件。条件が1つしかない(説明変数が切片のみからなる)場合は、数字の1と表記します。
# 確率分布；二項分布(binomial)
# 連結関数；S字(logit)

# 求める選択確率は、cbindで先に並べた方のものです。cbind(Light, Dark)としたので、Light(明るい方)を選択する確率を計算します。Dark(暗い方)を選択する確率は、｢1 - Lightを選択する確率｣となります。

# データを、横に増える(列が増える)方向に統合

# 説明変数の表記の仕方

# summary(r)を実行して、解析結果rの詳細を表示させます。

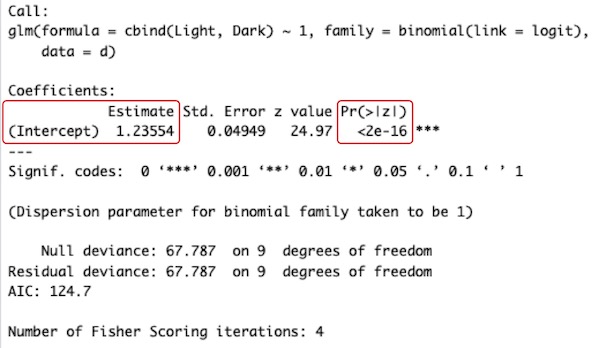
# 左の赤枠内にある(Intercept)が、回帰式y = e^b/(1 + e^b)の切片bの値です。b = 1.23554ですので、明るい方を選択する確率は、e^1.23554/(1 + e^1.23554) = 0.774787です。

#　右の赤枠内にあるのがP値です。切片(Intercept)の値(bの値)が有意に0と異なるのかどうかを示しています。｢e-｣とあるのは10のマイナス何乗かということです。｢2e-16｣は｢2 × 10^{- 16}｣です。切片(Intercept)(bの値)が有意に0と異なっているので、明るい方を選択する確率0.774787は、0.5(= e⁰/(1 + e⁰))とは有意に異なるということです。したがって、明るい方に移動しやすいといえます。

#　AICも出ているのですが、確率分布と連結関数の組合せは二項分布とS字の一択です。だから気にする必要はありません。

# 一般化線形モデルの命令文

3. 作図

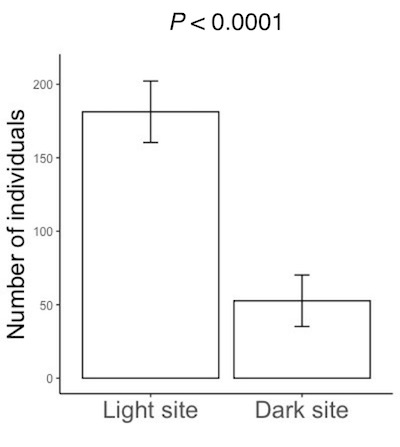
ミドリムシの走光性の作図の説明に従って作図をして下さい。軸の文字の説明を日本語にしたい場合は、ミドリムシの走光性の作図の説明に従って日本語にして下さい。そして、描いた図をPowerPoint等に読む込んで下さい。読み込む方法は図の保存･コピーを参照して下さい。

　PowerPoint等に読み込んで、P値を書き込みます。値があまりに小さい場合は、P < 0.0001といった書き方でよいです。